Summary keywords
The Working Group page contains links to individual members’ websites describing scientific work in more detail.
Please also see the CCP6 project archive: a fully amalgamated set of links will appear in the near future.
This page is under gradual construction. Fuller descriptions of particular projects, with links, will be added as the page is updated. Some sample topic headlines and illustrtions follow.
Electron collisions with molecules and molecular clusters. Description of the correlated electronic continua of molecules.
Differential cross sections for electron-pyrimidine scattering as a function of energy (see Mašin, Zdeněk and Gorfinkiel, Jimena D. (2016). Effect of the third π∗ resonance on the angular distributions for electron-pyrimidine scattering;. The European Physical Journal D, 70(7), article no. 151).
R-Matrix with Time Dependence (RMT)
The R-matrix with time-dependence (RMT) approach is the current state-of-the-art method for the description of general, multielectron atoms and ions in strong fields. Constructed using elements of forerunner codes HELIUM and TDRM, and built upon the R-matrix ‘inner region’ codes (originally developed for electron collision calculations), the RMT code uses a combination of B-spline basis and finite-difference techniques to model the multielectron wavefunction, and solve the time-dependent Schrodinger equation accurately and efficiently. The code is particularly well suited to the description of processes in intense long-wavelength (mid-IR) laser pulses, which have traditionally proved to be beyond the reaches of ab-initio theory.
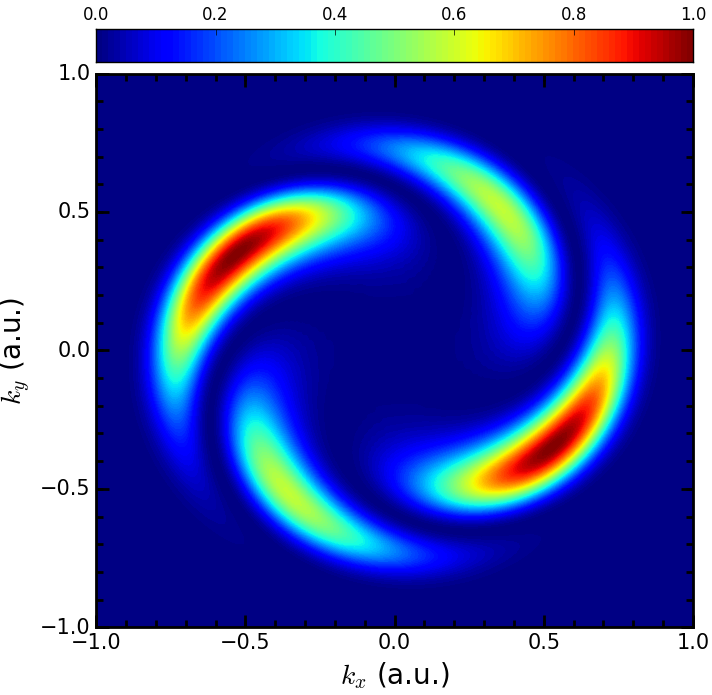
The code has been applied to model a range of cutting-edge experimental techniques, such as attosecond transient absorption spectroscopy and XUV-initiated high-harmonic generation.More recently, the code has been expanded to account for relativistic (spin-orbit) interactions, and arbitrarily polarised light both of which are unique capabilities in the field of time-dependent computational approaches to laser-atom interactions. The figure shows an application of the latter capability– producing so-called electron vortices using counter-rotating, circularly polarised light pulses to drive exotic dynamics in Helium.
Electron vortices in He (2018)
The RMT code also supports calculations of electronic dynamics in molecules with the necessary input data provided by the UKRMol+ codes. As a proof of principle, ionization rates for the H2 molecule have been calculated showing excellent agreement with previous results.
The image below [see O Hassouneh et al. Phys. Rev. A 91, 031404R (2015)]. shows the electron momentum distribution for the fluorine anion in an intense linearly polarised 1800 nm pulse. The low intensity rings apparent in the upper- and lower-half planes are signatures of the strong-field re-scattering process, whereby the photo-detatched electron is scattered from the neutral F atom as it is driven by the pulse.
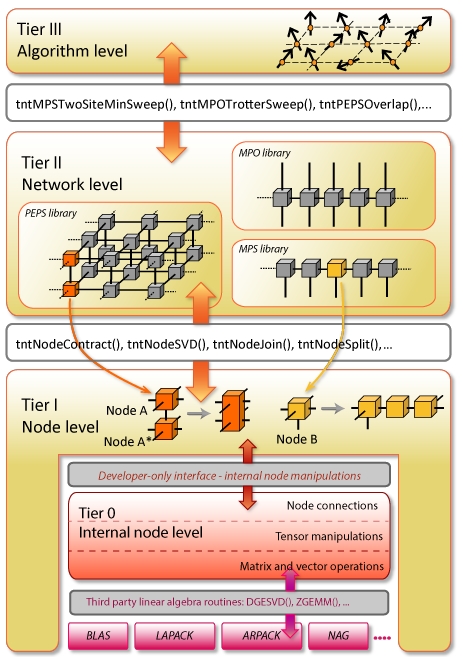
Tensor Network Theory
Tensor Network Theory (TNT) provides efficient and accurate methods for simulating strongly correlated quantum systems. It does this by encoding, as a network of tensors, the many-body wave function representing the system and the operators that act on it. TNT algorithms can then be broken down into a series of tensor operations. The TNT library project focuses on building highly optimised routines for manipulating tensors in a tensor network, which are completely general and do not depend on any network geometry, as well as routines that can be used to build the most common TNT algorithms. For an overview, please see: arXiv:1610.02244 [pdf, other] Tensor Network Theory – Part 1: Overview of core library and tensor operations, authors Sarah Al-Assam, Stephen R. Clark, Dieter Jaksch.
Spectroscopic molecular line lists for exoplanet & other atmospheres
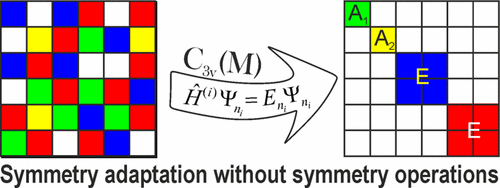
We present a general, numerically motivated approach to the construction of symmetry-adapted basis functions for solving ro-vibrational Schrödinger equations. The approach is based on the property of the Hamiltonian operator to commute with the complete set of symmetry operators and, hence, to reflect the symmetry of the system. The symmetry-adapted ro-vibrational basis set is constructed numerically by solving a set of reduced vibrational eigenvalue problems. In order to assign the irreducible representations associated with these eigenfunctions, their symmetry properties are probed on a grid of molecular geometries with the corresponding symmetry operations. The transformation matrices are reconstructed by solving overdetermined systems of linear equations related to the transformation properties of the corresponding wave functions on the grid. Our method is implemented in the variational approach TROVE and has been successfully applied to many problems covering the most important molecular symmetry groups. Several examples are used to illustrate the procedure, which can be easily applied to different types of coordinates, basis sets, and molecular systems. S.N.. Yurchenko, A. Yachmenev, and R.I. Ovsyannikov, Symmetry adapted ro-vibrational basis functions for variational nuclear motion: TROVE approach, J. Chem. Theory Comput., 13(9), 4368-4381 (2017).